Rectangular to Polar form & Polar to Rectangular form conversion
Phasor form conversion is the method of changing the representation form of a phasor. A Phasor is a rotating vector in a complex number form which expresses the magnitude and its phase. Sinusoidal signals with different magnitudes and phases, but the same frequency can be plotted on a phasor diagram; in a phasor diagram, the angular velocity (w) will be the same for all signals.
Phasors play a vital role in the analysis of AC circuits. Because it can be used to express the difference in magnitude and phase of multiple signals or parameters of the same signal. The complex form has two components, that is a real and imaginary part. In a phasor diagram, the real axis lays in the horizontal axis and the imaginary axis in the vertical axis. The phasor can be represented mathematically in three principal forms such as Rectangular form, trigonometrical form and Polar form.
The Rectangular form is represented by a real part (horizontal axis) and an imaginary (Vertical axis) part of the vector.

The Polar Form is represented by vector magnitude and angle with respect to the real axis. The vector value will be the modulus of the complex number. The value of the angle is represented either in degrees or radians, which is denoted by θ (Theta).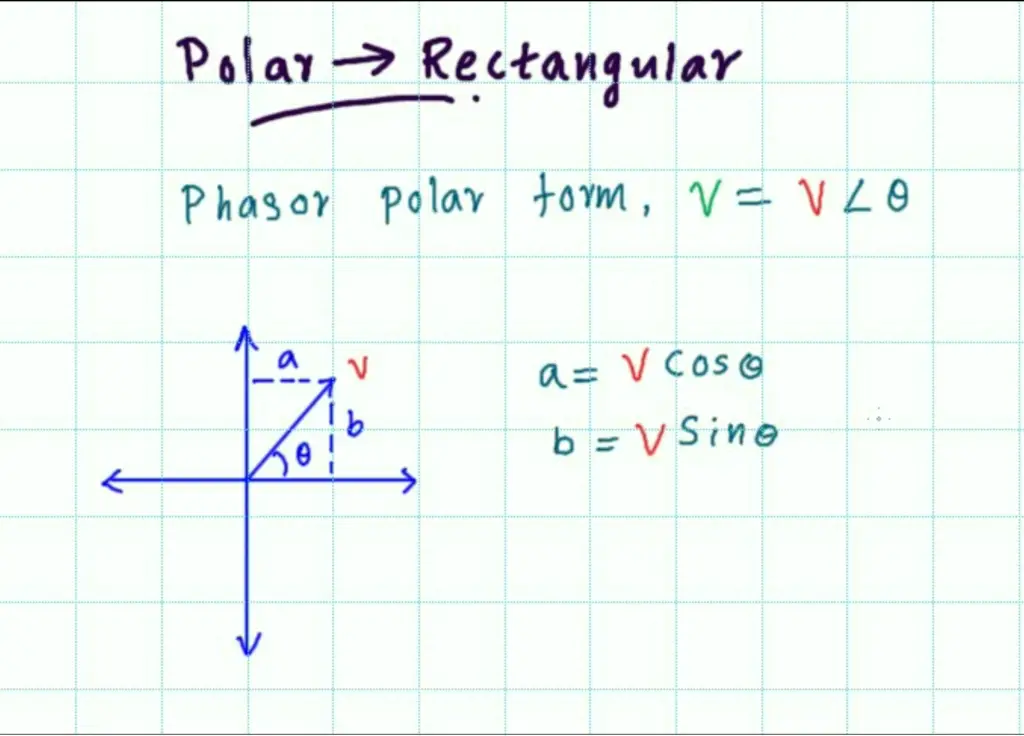
Rectangular to Polar Form Conversion
Rectangular form of a vector, v = a + jb. where a is the real axis value and b is the value of an imaginary axis.
To find the Phasor magnitude V, calculate the modulus of vector a + jb.
Magnitude of vector, V = √ a2 + b2.
To find the angle of a vector with respect to the horizontal axis, θ = tan-1 (b/a).
Phasor form of vector a+jb is, v = V∠θ.
Convert Polar to Rectangular Form
Polar form of the vector, v = V∠θ.
Phasor form of vector a+jb is, v = V∠θ.
To convert to rectangular form, calculate the horizontal and vertical axis values for the vector V.
a = V * cosθ
b = V* sinθ
Rectangular form of vector V∠θ is, v = a+jb.
j10 polar form
Rectangular form = 0 + j10 –> Polar form = 10∠90°
Hey thank you so much for this, no other online material was making as much sense as this did. So straightforward!
convert 5cosθ into polar form and what does θ represent here. What is the relation between θ in 5cosθ and θ1 in 5∠θ1
5∠θ, 5 is the length of the vector and θ is the angle made with the real axis (horizontal axis). 5cosθ gives you the value in real axis.
if θ = 45°, vector length = 5. Then 5cosθ = 5cos(45) = 3.53
thats the ‘theta’ symbol
Yes, theta “θ”.
convert 25sin2000t to the polar form . what is the angle ?
a = 25 cos2000t
b = 25 sin2000t
In polar form it is, 25∠2000t
θ = 2000t
what is the instantaneous value if the rectangular form is a+jb .and angular velocity is W
The resultant of the a+jb is the instantaneous value which is √(a^2 + b^2).
Convert
Z= 1/1+j to polar form