Measure temperature using Arduino and NTC thermistor
NTC (Negative Temperature Coefficient) thermistor has a characteristic of non-linear inverse varying resistance with respect to the temperature change. That is the resistance value decreases if the temperature of the thermistor is increased and it increases if the temperature is decreased. As it is nonlinear the temperature-resistance graph does not have a straight line. This rate of change of resistance versus temperature curve is indicated by a constant value called Beta value or Beta coefficient.
In code, the temperature of the NTC thermistor is calculated by using the Steinhart–Hart equation. It is considered the best mathematical expression to obtain the resistance vs temperature characteristic of an NTC thermistor. It can obtain the temperature values that are approximately equal to the actual values from the instantaneous resistance of the thermistor.
Steinhart–Hart β parameter equation, 1/T = 1/To + 1/B In(R/Ro)
T – Temperature
To – Nominal Temperature, 25 °C or 298.15 K
B – Beta co-efficient
R – Measured resistance of the thermistor
Ro – Nominal Resistance, resistance at temperature T0 is 25 °C or 298.15K
The temperature value in kelvin for the respective resistance (R) of NTC thermistor, T = 1 / (1/To + 1/B In(R/Ro))
A thermistor module or a standalone thermistor both can be used to measure the temperature.
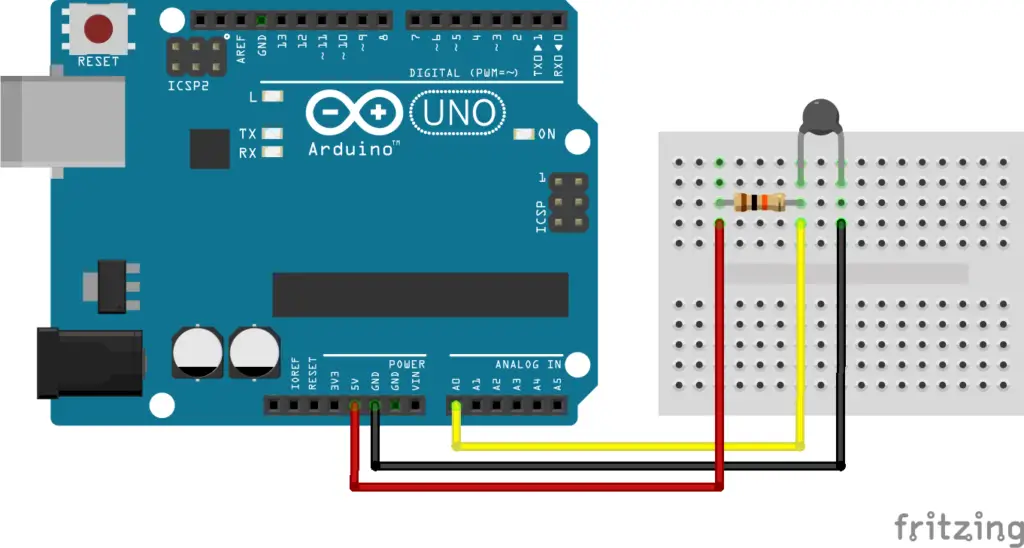
In the below standalone circuit, a 50K thermistor is connected in series with a 10k resistor, and a 5V supply is connected across the series circuit. The analog input of the Arduino is connected across the thermistor, so the resistance of the thermistor can be calculated from the voltage drop measured across it.
In a thermistor module, the analog output of the module is connected to the analog pin of the Arduino which has the same circuit as the above one. It also has the analog input of the Arduino connected across the NTC thermistor with a 10k series resistor and connected across a 5V supply.
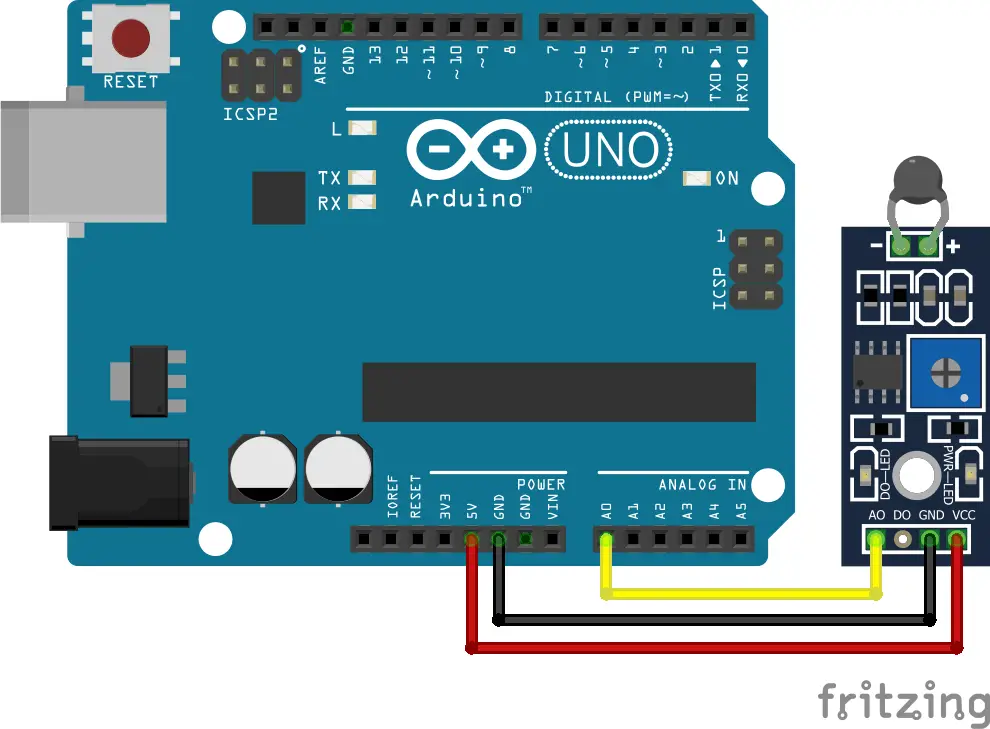
The only difference of the module is it has an additional digital output with a threshold setting that can be adjusted by the potentiometer. It gives a HIGH state output if the temperature is below the threshold and the output switch to LOW when the temperature is above the threshold. It also has a DO-LED which works inverse to the digital output; LED ON when the output is LOW and LED OFF when output is HIGH.
In both the above circuits, the thermistor is in series with a resistor of a fixed value. Hence the voltage across the thermistor will be proportional as per the voltage division of series resistor circuits. So, using the voltage division formula, the instantaneous value of the resistance is calculated from the voltage measured across the thermistor.
VRT = V * RT/RS + RT by rearranging this equation the expression for RT can be obtained as, RT = VRT * Rs / (V – VRT).
Rs – Series resistor
RT – Instantaneous resistance value of the thermistor
V – Total voltage across the series resistor
VRT – Voltage across the thermistor
Then this resistor value can be applied in the Steinhart–Hart beta parameter equation which gives the temperate value in kelvin. From kelvin, the temperature values can be easily converted to either Celsius or Fahrenheit by using the below equations.
Kelvin to Celsius, Tcelsius= TKelvin – 273.15
Celsius to Fahrenheit, TFahrenheit = Tcelsius x 9.0 / 5.0 + 32.0
Kelvin to Fahrenheit, TFahrenheit = (TKelvin – 273.15) x 9.0 / 5.0 + 32.0
Code
int Ro = 50, B = 3950; //Nominal resistance 50K, Beta constant int Rseries = 10;// Series resistor 10K float To = 298.15; // Nominal Temperature void setup() { Serial.begin(9600); } void loop() { /*Read analog outputof NTC module, i.e the voltage across the thermistor */ float Vi = analogRead(A0) * (5.0 / 1023.0); //Convert voltage measured to resistance value //All Resistance are in kilo ohms. float R = (Vi * Rseries) / (5 - Vi); /*Use R value in steinhart and hart equation Calculate temperature value in kelvin*/ float T = 1 / ((1 / To) + ((log(R / Ro)) / B)); float Tc = T - 273.15; // Converting kelvin to celsius float Tf = Tc * 9.0 / 5.0 + 32.0; // Converting celsius to Fahrenheit Serial.println((String)"Temperature in celsius :" + Tc + "°C"); Serial.println((String)"Temperature in Fahrenheit :" + Tf + "°F"); Serial.println(" "); delay(1000); }
Both the module and circuit have a 50K NTC thermistor which has a nominal resistance of 50Kohms at nominal temperature value T0 25 °C or 298.15K, also the series resistance is 10K in both circuits. So change the “Ro” value and Beta value in the code with the corresponding thermistor used in the circuit and “Rseries with series resistance value. In the code the resistance values are in kilo-ohms, so just use 10 or 50 for 10K or 50K values.
hello, I am a french person, Canadian. My sketch is easier, I think, and exactly. I use the calibrated Steinhart-Hart coefficient for the thermistor and I do a regression: y=a+blnR ; a=226.0353 ,b=-21.8271 .I include the sketch.
int Rseries = 10850 ;
float To = 298.15 ;
void setup(){
Serial.begin(9600);
}
void loop() {
/*Read analog outputof NTC module,
i.e the voltage across the thermistor */
float Vi = analogRead(A0) *(5.0/1023.0);
Serial.print(Vi);
delay(500);
Serial.println(” “);
float R = (Vi * Rseries) / (5 -Vi);
Serial.print(R);
delay(500);
Serial.println( ” “);
/* Use R value in steinhart and hart equation
Calculate temperature value in kelvin */
float Tc =( -21.8271*log ( R)+226.0353 );
Serial.print(Tc);
delay (500);
Serial.println(” “);
float Tf = Tc * 9.0 / 5.0 + 32.0 ;
Serial.println((String)”Temperature in celcius : ” + Tc + “C”);
Serial.println((String)”Temperature in Fahrenheit : ” + Tf +”F”);
Serial.println(” “);
delay(1000);
}
The serie resistance is 10000 ohm but you need toput 10850 =R series in code.
thank you for the formula provided.
Thank you. It helped me.
float Vi = analogRead(A0) * (5.0 / 1023.0);
should be
float Vi = 5.0 – analogRead(A0) * (5.0 / 1023.0);